Теория дифракции


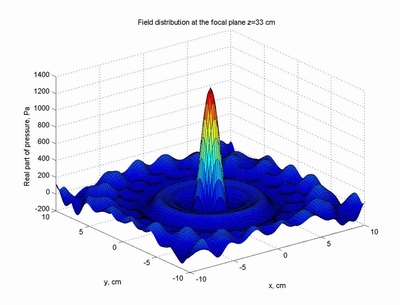
Ультразвуковая антенна, спроектированная в лаборатории, и расчет поля в ее фокальном пятне

Теория дифракции - область математической физики, посвященная расчету волновых полей, создаваемых специальными устройствами (антеннами) и взаимодействующих с различными препятствиями. Обычно имеются в виду электромагнитные или акустические поля. Своим развитием теория дифракции обязана потребностям прежде всего радиолокации и гидролокации. Кроме того, результаты теории дифракции используются в оптике, СВЧ - электронике, дефектоскопии и еще много где.

В типичной ситуации геометрия антенны или препятствия столь сложна, что аналитически решить соответствующую задачу невозможно. Поэтому для расчета полей применяют приближенные методы. Обычно такой метод состоит в том, что антенну или рассеиватель представляют как совокупность простых элементов (полуплоскость, конус, сфера, клин) и рассматривают последовательность актов рассеяния на каждом из этих элементов. Описание рассеяния на каждой из элементарных форм составляет каноническую задачу дифракции.

Если говорить более предметно, мы занимаемся задачами дифракции на конечных дифракционных решетках, конусах многоугольного сечения, клиньях.

В нашей лаборатории были получены следующие результаты:

Установлено, что в диаграмме направленности для широкого класса излучателей можно разделить зависимость от угла падения и угла отражения, т.е. функцию двух переменных переписать в виде комбинации функций от одной переменной.
Показано, что для некоторых задач теории дифракции (полоса, дифракционная решетка, уголковый отражатель) поле удовлетворяет системе дифференциальных уравнений первого порядка, т.н. координатным уравнениям. Этот результат является обобщением метода разделения переменных.
Для тех же задач выведены обыкновенные дифференциальные уравнения, которым удовлетворяют диаграммы направленности ("спектральные уравнения"). Этот результат обобщает метод Винера-Хопфа.

Основные публикации

A.V.Shanin, Diffraction of a plane wave by two ideal strips // Q.Jl Mech. Appl. Math. V. 56, No 2, pp. 187-215 (2001)
R.V.Craster, A.V. Shanin, E.M.Doubravsky, Embedding formulae in diffraction theory // Proc.Roy.Soc.Lond.A (2003) V.459, 2475-2496. (PDF file)
R.V.Craster, A.V.Shanin, Embedding formula for diffraction by wedge and angular geometries // PRSLA, (2005) V.461, 2227-2242 (PDF file)
A.V.Shanin, A generalization of the separation of variables method for some 2D diffraction problems // Wave Motion, V.37, N.3, pp. 241-256 (2003)
A.V.Shanin, E.M.Doubravsky, To commutative factorization of algebraic matrices. Submitted to PRSLA PDF file