В последние годы все большее внимание акустиков уделяется информационным возможностям нелинейного акустического параметра - достаточно новому методу характеризации среды. Изначально теоретические модели строились на предположении о том, что при распространении акустической волны через жидкую среду изменение давления и плотности линейно по отношению друг к другу. Тем не менее, первые же попытки создания источников мощных акустических сигналов (1950-е годы), привели к выводу, что учет нелинейности законов гидродинамики и состояния среды принципиально важен. Оказалось, что при больших величинах акустических давлений отклонение от линейной зависимости становится настолько велико, что оно выходит на передний план: происходит искажение формы волны, расширение спектра частот, нелинейное поглощение (которое на порядки превышает обычное поглощение), помимо этого имеет место нелинейное взаимодействие волн между собой (не соблюдается принцип суперпозиции) и т.д. Исследование проявлений нелинейного поведения акустических волн показало, что процесс распространения упругих волн нелинеен всегда, и основной причиной этому является среда (сила взаимодействия между молекулами среды непропорциональна силе сближения или отдаления молекул), в которой происходит распространение волны. Степень отклонения от линейной зависимости принято характеризовать нелинейным параметром. Таким образом, с открытием роли нелинейности, значение акустического нелинейного параметра стало дополнительным параметром характеризации упругих свойств вещества, наряду со значениями таких привычных параметров, как скорость звука, поглощение или плотность.
Примером преимуществ использования нелинейного параметра для целей медицинской диагностики являются данные, приведенные в [Zhang D., Gong X.F. Experimental investigation of the acoustic nonlinearity parameter tomography for excised pathological biological tissues // Ultrasound in Med. & Biol. 1999. V. 25. N. 4. P. 593-599] для восьми различных патологий свиной печени, что позволяет непосредственно сравнить относительное отличие линейных и нелинейного параметров в больных и здоровых тканях. Относительное изменение скорости звука составляет 2-3.8%, плотности - меньше 1%, в то же самое время отклонение нелинейного параметра находится на уровне 9-20%. Таким образом, в системах томографии нелинейного параметра эффективное изменение значения диагностируемого параметра, по сравнению с его фоновым значением, в несколько раз превышает подобное отношение для систем томографии, дающих количественное распределение линейных характеристик.
Методы, применяемые в настоящее время для нахождения нелинейных характеристик объекта, основаны, в большинстве случаев, на лучевом приближении, использующем картину роста второй гармоники (или сигнала комбинационной частоты) по мере распространения волны [X.F.Gong, Y.S.Yan, D.Zhang, H.L.Wang. The study of acoustic nonliniarity parameter tomography in reflection mode // Nonlinear Acoustics at the Beginnings of the 21st Century. Moscow: MSU, Faculty of Physics, 2002. V.1. P.469-472. D. Zhang, X. Chen, X. Gong. Acoustic nonlinearity parameter tomography for biological tissues via parametric array from a circular piston source. Theoretical analysis and computer simulations // J. Acoust. Soc. Am. 2001. V.109. N3. P.1219-1225], либо взаимодействие в луче высокочастотной пробной волны с мощным импульсом накачки [T.Sato, K.Yamashita, H.Ninoyu et al. Imaging of acoustical nonlinear parameters and its medical and industrial applications // Acoustical Imaging. New York: Plenum Press, 1993. V.20. P.9-18]. Хотя реализация подобных томографических систем достаточно проста, они обладают такими существенными недостатками, как сравнительно невысокое пространственное разрешение (0.3-1см) и длительное время сбора томографических данных. В связи с вышесказанным, задача поиска новых методов томографирования нелинейного параметра продолжает оставаться актуальной.
В лаборатории разработан новый волновой подход к решению задачи восстановления распределения значения нелинейного параметра. Метод основан на нелинейном взаимодействии кодированных акустических волн (эффект рассеяния звука на звуке [Зарембо Л.К., Красильников В.А. Введение в нелинейную акустику // М.: Изд-во "Наука", 1966. С. 520]) в присутствии распределенных неоднородностей нелинейного параметра а, также на применении сложной обработки зарегистрированных данных (согласованной фильтрации).
Предложенный метод, являющийся обобщением [Буров В.А., Гуринович И.Е., Руденко О.В., Тагунов Е.Я. "Реконструкция пространственного распределения параметра нелинейности и скорости звука в акустической нелинейной томографии". Акустич. журн. Изд-во РАН, 1994, Т.40, N 6, С.421-429] на случай немонохроматических волн, кратко можно описать следующим образом. Благодаря нелинейным эффектам, в зоне пересечения акустических волн происходит их взаимодействие, результатом которого являются воны на суммарных и разностных частотах. Ввиду того, что взаимные задержки на распространение каждой волны до различных точек пространства разные, а сами первичные волны - кодированные, получается, что от каждого элементарного нелинейного "источника" порождается уникальная (в плане кодировки) волна на суммарной и разностной комбинационной частоте. Сигналы от всей области взаимодействия первичных волн (т.е. от всех элементарных нелинейных "источников") регистрируются одним или несколькими приемниками. Что интересно - несмотря на смешение всех этих сигналов в общий сигнал рассеяния (эти сигналы суммируются приемником), информация о пространственном распределении нелинейных источников не утрачивается. Таким образом, рассчитав взаимные задержки на распространение первичных сигналов до определенной точки пространства, можно вычислить код сигнала, который рождается в этой точке нелинейным источником, что в свою очередь, благодаря применению согласованной фильтрации, позволяет определить "силу" этого источника и выделить его вклад в принятый сигнал, т.е. рассчитать значение нелинейного параметра в этой точке.
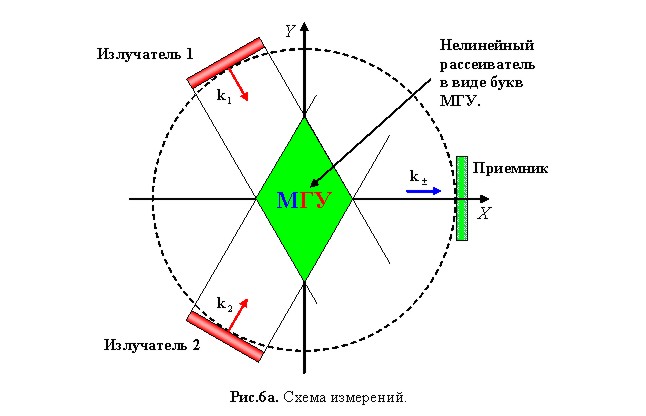
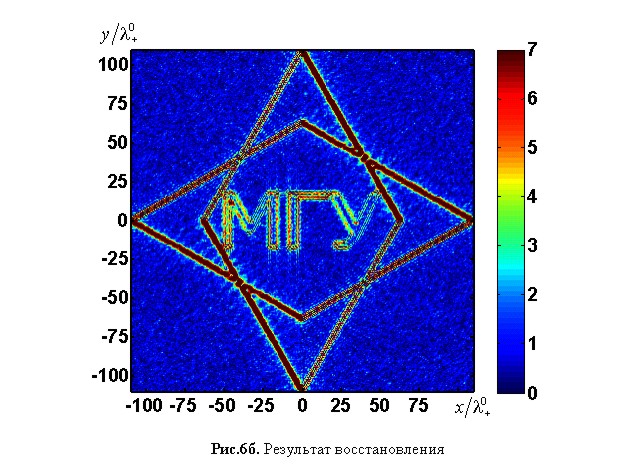
Итак, благодаря примененной методике получена реальная возможность восстановления двумерного распределения нелинейного параметра при использовании всего нескольких преобразователей (рис.6а). Результат такого восстановления приведен на рис.6б.
Более подробно материалы этих исследований, включающие компьютерное моделирование и физический эксперимент по определению акустического нелинейного параметра второго порядка, изложены в следующих работах:
- Буров В.А., Евтухов С.Н., Ткачева А.М., Румянцева О.Д. Акустическая томография нелинейного параметра с помощью малого числа преобразователей // Акустический журнал. 2006. Т. 52. № 6. С. 760?776.
- С.А.Береза, В.А. Буров, С.Н. Евтухов. Модельные эксперименты по акустической томографии нелинейного параметра // Акустич. журн. 2008. Т.54. №4 С.522-534.
Акустический нелинейный параметр второго порядка, ответственный за рождение вторых гармоник и появление суммарных и разностных комбинационных частот распространяющихся в среде волн, на настоящий момент изучен достаточно хорошо. Акустический нелинейный параметр третьего порядка изучен крайне мало, и он является новой характеристикой для медицинской диагностики. В настоящее время в группе ведется работа над созданием прототипа медицинского нелинейного томографа, позволяющего восстановить пространственное распределение акустических нелинейных параметров как второго, так и третьего порядков. Применение кодированных первичных сигналов с последующей корреляционной обработкой регистрируемого комбинационного сигнала позволяет восстановить полное изображение объекта в результате всего одного эксперимента с использованием малого числа преобразователей - трех излучателей и одного приемника. Предложена зеркальная система, состоящая из двух соосных конических акустических зеркал и позволяющая преобразовать фронт волны от цилиндрического преобразователя в однородный квазиплоский пучок с большой шириной, близкой к реальным требованиям медицинской диагностики. В настоящее время проведены первые физические эксперименты (рис.2, рис.3).
Основными преимуществами разрабатываемого нелинейного томографа являются следующие:
а) Возможность восстановления количественных значений принципиально новой для медицинской диагностики величины - акустического нелинейного параметра третьего порядка.
б) Малое количество акустических преобразователей, что не требует больших денежных затрат на их изготовление.
в) Измерения проводятся в результате всего одного-двух экспериментов, что занимает не более минуты и не требует изменения ориентации преобразователей; тем самым, исключаются погрешности, вносимые непроизвольными движениями пациента.
г) При использовании в качестве всех трех первичных сигналов, которыми зондируют объект, широкополосных кодированных волн, открывается возможность не только двумерного, но и трехмерного томографирования.
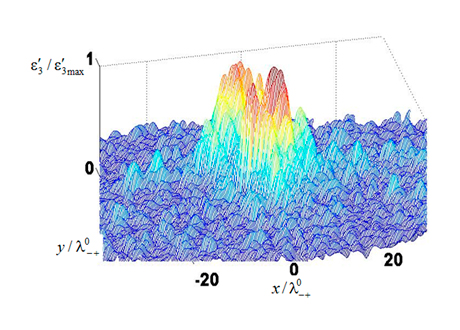
Рис.2. Результат восстановления значения эффективного нелинейного параметра в столбике свиного сала размером 2см х 2см.
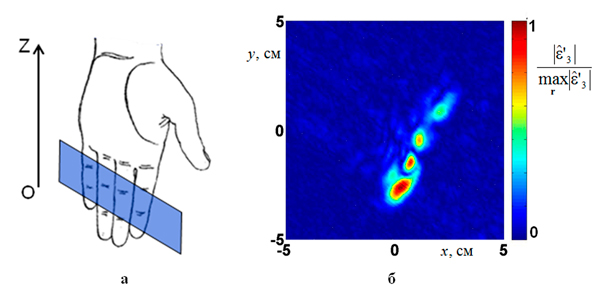
Рис.3. Поперечное сечение четырех пальцев человека, сложенных вместе: ориентация пальцев в пространстве (а) и результат восстановления (б).
Основные публикации по проблеме нелинейного томографирования третьего порядка:
- В.А. Буров, А.А. Шмелев, О.Д. Румянцева. Томография пространственного распределения рассеивателя в нелинейных процессах третьего порядка // Известия Российской Академии Наук. Серия Физическая. 2008. Т.72. №1. С.92-99.
- Burov V.A., Evtukhov S.N., Shmelev A.A., Rumyantseva O.D. Tomography of spatial distribution of scatterer in nonlinear processes of the second and third orders // Nonlinear Acoustics - Fundamentals and Applications (Proceedings of 18th International Symposium on Nonlinear Acoustics). Edited by B.O.Enflo, C.M.Hedberg, and L.Kari (American Institute of Physics, Melville, New York, 2008). P.440-443.
- Буров В.А., Шмелев А.А. численное и физическое моделирование процесса томографирования на основе акустических нелинейных эффектов третьего порядка // Акуст. журн. 2009. Т.55. №4-5. С.466-480.
- V.A. Burov, A.A. Shmelev, O.D. Rumyantseva. Numerical and physical modeling of tomography process based on third-order nonlinear acoustical effects // Acoustical Imaging. Ed. M.P.André, J.P.Jones, H.Lee. Dordrecht, Heidelberg, London, New York: Springer Science+Business Media B.V. 2011. V.30. P. 379-388.
- Буров В.А., Крюков Р.В., Румянцева О.Д., Шмелев А.А. Проблемы использования нелинейных коллинеарных процессов в акустической томографии третьего порядка // Акуст. журн. 2012. Т. 58. № 1. С. 57-79.
- Крюков Р.В. Роль возмущений энтропии в задачах нелинейной акустической томографии третьего порядка // Акуст. журн. 2012. Т. 58. № 2. С. 184-192.
- Буров В. А., Шмелев А.А., Зотов Д.И. Прототип томографической системы, использующей акустические нелинейные эффекты третьего порядка // Акуст. журн. 2013. Т. 59. № 1. С. 31-51.
В заключение следует подчеркнуть, что томографическое восстановление распределения нелинейного акустического параметра представляет собой самостоятельный вид обратных задач. Оно тесно связано с необходимостью одновременной оценки распределения линейных и нелинейных параметров среды. Строгого математического решения этой проблемы, аналогичного решениям обратных задач линейного рассеяния, в настоящее время не существует. Более того, рассмотрение простейшей обратной задачи при наличии только нелинейных неоднородностей приводит к выводу о сильнейшей избыточности данных рассеяния и, отсюда, к множеству возможных "эвристических" путей ее решения. Таким образом, обозначенная проблема очень многогранна, и уровень ее понимания далек пока еще от желаемого. Поэтому необходим поиск перспективных, с практической точки зрения, методов количественной оценки картины распределения линейных и нелинейных параметров среды.